Property Description
One bedroomed terraced property pleasantly positioned on West Road in Bishop Auckland. Located just a short distance from the town centre, within walking distance to Kynren, the Faith Museum, Auckland Castle and the Spanish Art Gallery. This central location offers easy access to a variety of local amenities such as both primary and secondary schools, supermarkets, local shops, cafes, retail stores and restaurants. Further facilities are available within the Town as well as at Tindale's ever expanding retail park, which hosts a range of high street stores, retail shops, food outlets as well as its new cinema/bowling and shopping complex due to open in summer 2024. There is an extensive public transport system in the area via both bus and train, whilst the A689 is nearby leading to the A1(M) both North and South, ideal for commuters.
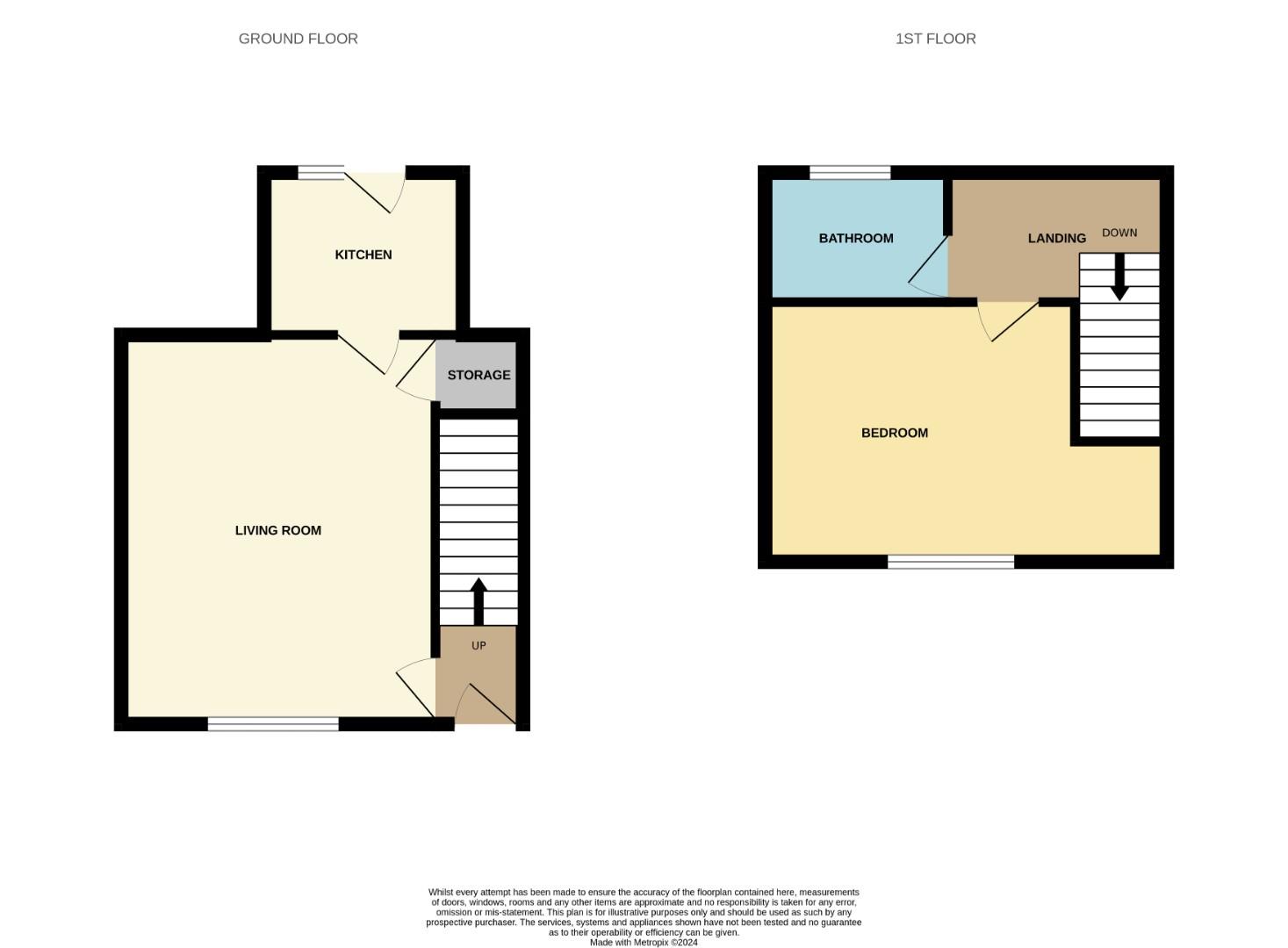
In brief, the property comprises; an entrance hall leading through into the living room and kitchen to the ground floor. The first floor contains the master bedroom and bathroom. Externally, the property to the rear has an enclosed yard.
In brief, the property comprises; an entrance hall leading through into the living room and kitchen to the ground floor. The first floor contains the master bedroom and bathroom. Externally, the property to the rear has an enclosed yard.
Living Room (4.8m x 3.9m)
Generous main reception room with window to front offering plenty of natural light.
Kitchen (2.5m x 2.0m)
Fitted with a range of units and space for appliances.
Bedroom (3.3m x 3.2m)
An impressive king sized bedroom with window to front.
Bathroom (2.2m x 1.6m)
Comprising a low level WC, wash hand basin and panelled bath.
External
Externally to the rear is an enclosed yard with outhouse for storage.
Material Information
- Tenure: Freehold
Standout Features
- ONE BEDROOM
- TERRACED
- SPACIOUS
- CLOSE TO TOWN CENTRE
- LOTS OF POTENTIAL
- ENCLOSED YARD
- GAS CENTRAL HEATING
- EPC GRADE TBC
Mortgage calculator
Calculate Your Stamp Duty
Results
Stamp Duty To Pay:
Effective Rate:
| Tax Band | % | Taxable Sum | Tax |
|---|
West Road, Bishop Auckland
Want to explore West Road, Bishop Auckland further? Explore our local area guide
Struggling to find a property? Get in touch and we'll help you find your ideal property.
Bishop Auckland
147-149 Newgate Street
, Bishop Auckland, County Durham
, DL14 7EN
