St. Christophers Drive, Tamworth

Standout Features

MOBILE HOME
TWO BEDROOMS
BIG GARDEN PLOT
FREEHOLD
MUST VIEW
POPULAR LOCATION
ACCESSIBLE PROPERTY

Property Description

HUNTERS OF TAMWORTH are delighted to be offering FOR SALE this well presented, two bedroom park home located in the pleasant location of Two Gates.
This charming property benefits from being close to local amenities, transport and commuter links, providing access to Tamworth town centre hosting all necessities. This property is perfect for those looking to downsize or are looking for an easily accessible property.

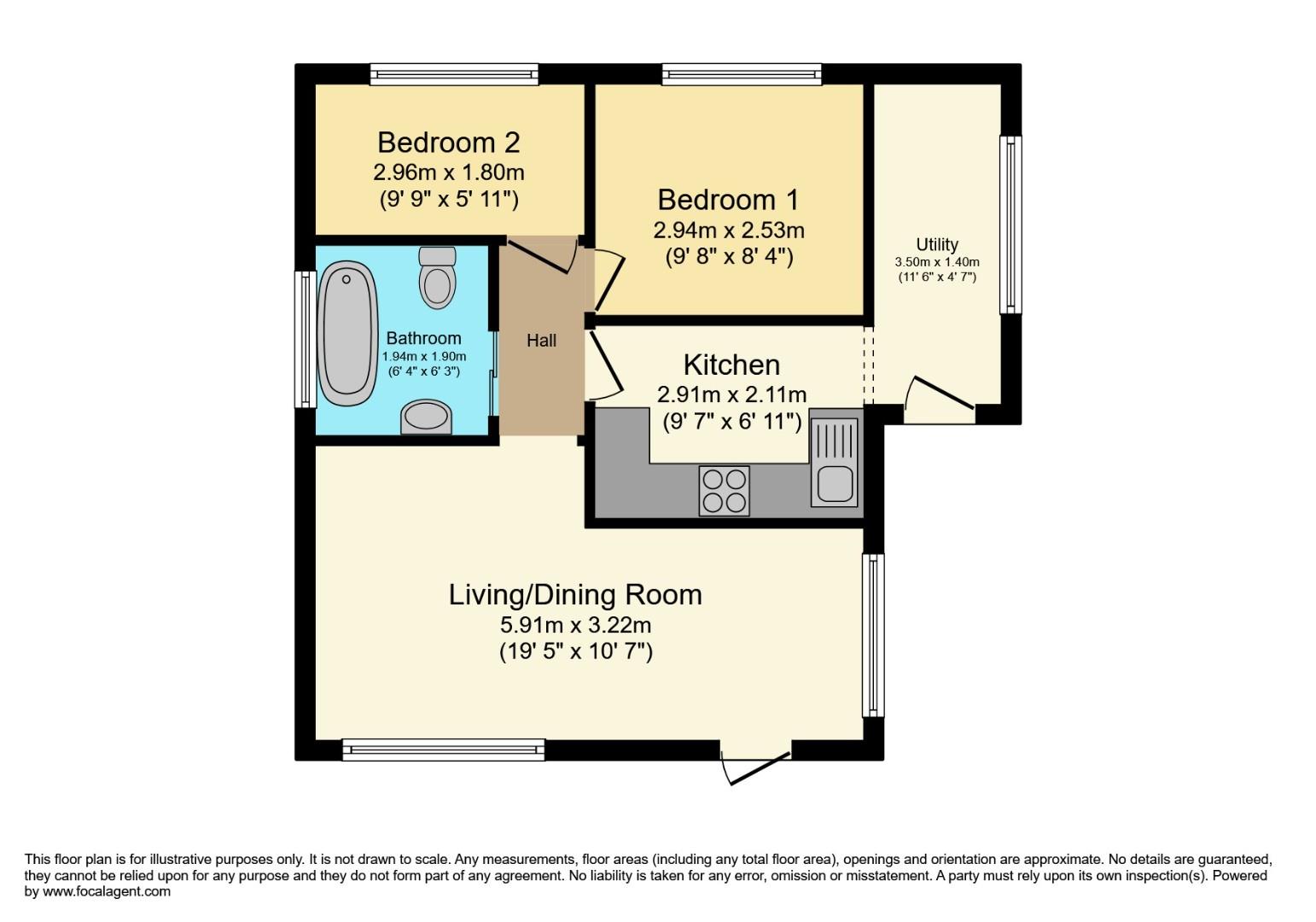
In brief the property comprises; utility room/side porch, kitchen, living/dining room, two bedrooms, bathroom and private wrap around garden and patio area. The property has allocated parking.

Utility

Double glazed window to side, wood effect flooring, door to front, radiator, power points

Kitchen (2.74m 2.13m x 2.11m)

Double glazed window to front, wood effect flooring, tiled splash back, wall and base units, built in oven and hob, stainless steel sink and drainer, plumbing for washing machine, ceiling light, radiator, power points

Living/Dining (5.79m 1.52m x 3.05m 2.13m)

Double glazed window to front, door to front, carpeted flooring, feature fireplace, radiator, ceiling light, power points

Bedroom One (2.74m 2.44m x 2.44m 1.22m)

Double glazed window to rear, carpeted flooring, ceiling light, radiator, owner points

Bedroom Two (2.74m 2.74m x 1.80m)

Double glazed window to rear, wood effect flooring, ceiling light, radiator, power points

Bathroom (1.83m 1.22m x 1.83m 0.91m)

Double glazed window to side, low flush WC, sink and vanity unit, corner bath with shower overhead, ceiling light, radiator

Garden

Wrap around, big plot, low maintenance,, paved patio, astro turf, paved area to rear

Additional Information

Tenure:	Freehold
Council Tax Band:	A

Rooms

Utility

Double glazed window to side, wood effect flooring, door to front, radiator, power points

Kitchen

Living/Dining

Double glazed window to front, door to front, carpeted flooring, feature fireplace, radiator, ceiling light, power points
5.79m 1.52m x 3.05m 2.13m (19' 5" x 10' 7")

Bedroom One

Double glazed window to rear, carpeted flooring, ceiling light, radiator, owner points
2.74m 2.44m x 2.44m 1.22m (9' 8" x 8' 4")

Bedroom Two

Double glazed window to rear, wood effect flooring, ceiling light, radiator, power points
2.74m 2.74m x 1.80m (9' 9" x 5'11")

Bathroom

Double glazed window to side, low flush WC, sink and vanity unit, corner bath with shower overhead, ceiling light, radiator
1.83m 1.22m x 1.83m 0.91m (6' 4" x 6' 3")

Garden

Wrap around, big plot, low maintenance,, paved patio, astro turf, paved area to rear

Mortgage calculator