Property Description
Hunters Crookes are delighted to market this FIVE bedroom TWO bathroom bay windowed student licenced HMO situated in the popular and much sought after area of Broomhill. The property is currently tenanted until July 2024, and is generating approximately £1925 pcm. With some improvement to the accommodation this figure could be increased.
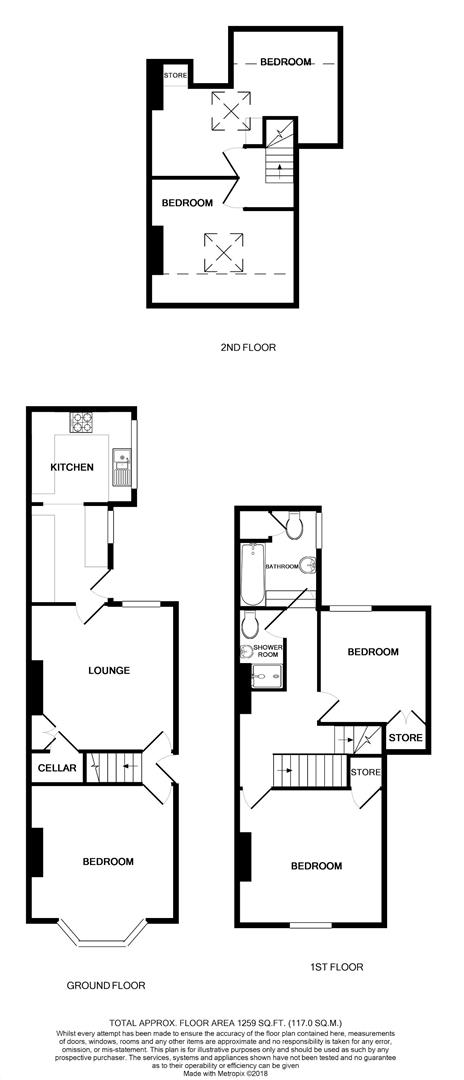
The accommodation briefly comprises; side entrance lobby with stairway access to the first floor, front bay windowed bedroom one, rear living room and extended kitchen to the rear. On the first floor are two bedrooms, bathroom and shower room with a further two double bedrooms to the second floor. External there is a garden to the rear.
The property is situated in Broomhill and is less then a mile away Sheffield University.
GENERAL REMARKS
TENURE
The property is Long leasehold with a term of 800 years from 1949 at a ground rent of £3.74 per annum.
RATING ASSESSMENT
We are verbally advised by the Local Authority that the property is assessed for Council Tax purposes to Band B.
VACANT POSSESSION
Vacant possession will be given on completion and all fixtures and fittings mentioned in the above particulars are to be included in the sale.
MORTGAGE FACILITIES
We should be pleased to advise you in obtaining the best type of Mortgage to suit your individual requirements.
YOUR HOME IS AT RISK IF YOU DO NOT KEEP UP REPAYMENTS ON A MORTGAGE OR OTHER LOANS SECURED ON IT.
The accommodation briefly comprises; side entrance lobby with stairway access to the first floor, front bay windowed bedroom one, rear living room and extended kitchen to the rear. On the first floor are two bedrooms, bathroom and shower room with a further two double bedrooms to the second floor. External there is a garden to the rear.
The property is situated in Broomhill and is less then a mile away Sheffield University.
GENERAL REMARKS
TENURE
The property is Long leasehold with a term of 800 years from 1949 at a ground rent of £3.74 per annum.
RATING ASSESSMENT
We are verbally advised by the Local Authority that the property is assessed for Council Tax purposes to Band B.
VACANT POSSESSION
Vacant possession will be given on completion and all fixtures and fittings mentioned in the above particulars are to be included in the sale.
MORTGAGE FACILITIES
We should be pleased to advise you in obtaining the best type of Mortgage to suit your individual requirements.
YOUR HOME IS AT RISK IF YOU DO NOT KEEP UP REPAYMENTS ON A MORTGAGE OR OTHER LOANS SECURED ON IT.
Material Information
- Tenure: Leasehold
- Lease Years Remaining: 726
- Ground Rent: £4 per year
Standout Features
- FIVE BEDROOMS
- TWO BATHROOMS
- IDEAL FOR INVESTORS
- GREAT LOCATION
- ACHIEVABLE RENT OF £1925PCM (£88PPPW)
- LICENCED HMO
- REAR GARDEN
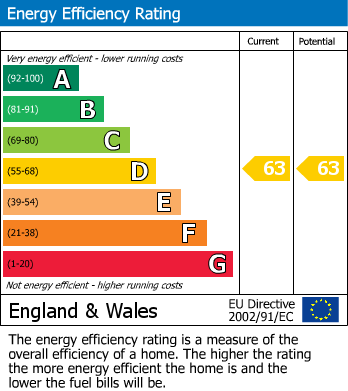
- ENERGY PERFORMANCE RATING D
Mortgage calculator
Calculate Your Stamp Duty
Results
Stamp Duty To Pay:
Effective Rate:
| Tax Band | % | Taxable Sum | Tax |
|---|
Crookes Road, Broomhill, Sheffield, S10 5BD
Want to explore Crookes Road, Broomhill, Sheffield, S10 5BD further? Explore our local area guide
Struggling to find a property? Get in touch and we'll help you find your ideal property.
Sheffield Crookes
208 Crookes
, Sheffield, South Yorkshire
, S10 1TG
